the three medians of a triangle intersect at the

buskey March 27, 2022 intersect , the , triangle Comment

Because there are three vertices there are of course three possible medians. Centroid If you draw all three medians they will intersect at one point called the centroid.

Medians And Altitudes Of A Triangle

Therefore the three medians of any triangle meet at a common point known as the centroid that cuts each median into a ratio of 2.

. But others have not been honest enough. The sum of squares of the medians of a triangle equals three-fourths of the sum of squares of the sides of the triangle. Median of a triangle.

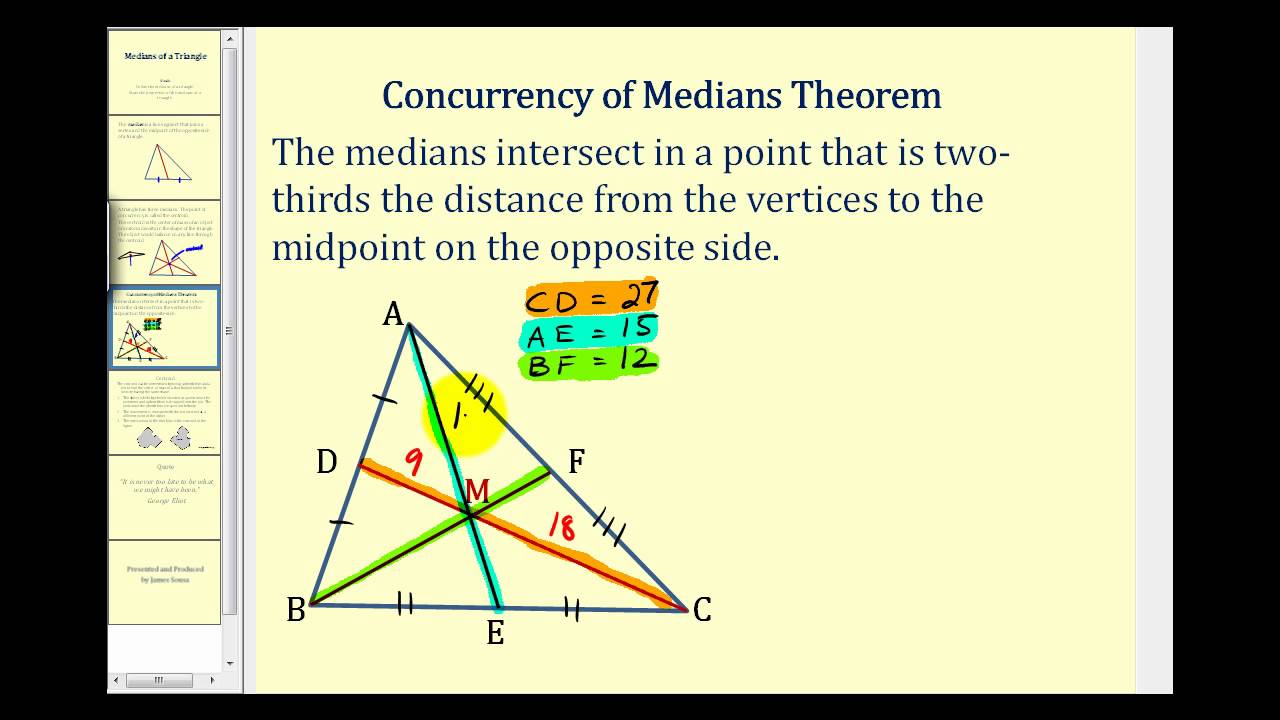
The unique point equidistant from the vertices is the center of the circle passing through them so the three sides of the triangle are secants of the circle and the center lies on the axis of each side the orthogonal line passing through the. Words The medians of a triangle intersect at the centroid a point that is two thirds of the distance from each vertex to the midpoint of the opposite side. Every triangle has exactly three medians one from each vertex and they all intersect each other at the triangles centroid.

We have not only proved our theorem but we have learned something about where this point is located. The three median of any triangle are concurrent. Regardless of the shape or size of a triangle its three medians meet at a single point.

A segment from a vertex to the midpoint of the opposite side. See also how are robots different from other machines. Moreover AG 2GD BG 2 GE and CG 2GF.

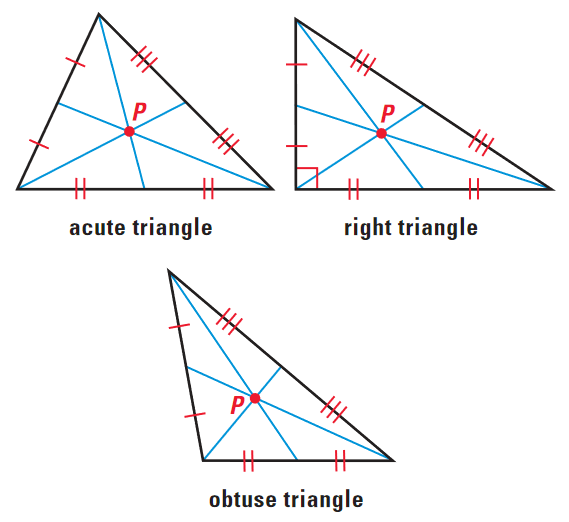
The point of concurrency of medians is called the centroid of the triangle. An isosceles triangle has _____sides. A point on the interior of a triangle in which the three medians of the triangle intersect.

In ABC the measures of the three angles are represented by 9 x 3 x-6 and 11 x 2. Please dont take this harshly -- I think its a very nice idea. This means that if you were to cut out the triangle the centroid is its center of gravity so you could balance it there.

When written in the correct order the two-column proof below describes the statements and justifications for proving the three medians of a triangle all intersect in one point. Here I will simply state the theorems formal proofs are omitted but are part of secondary school mathematics 1. The three medians of ΔABC intersect at a common point.

The three medians divide the triangle into 6 smaller triangles of similar area. There are a number of theorems that we need to look at before we doing the proof. If you draw all three medians they will intersect at one point called the centroid.

The centroid is the balancing point of a triangle. The point of intersection of all three medians is called the centroid of the triangle. The three medians of ΔABC intersect at a common point.

Every triangle has exactly three medians one from each vertex and they all intersect each other at the triangles centroid. Statements Justifications Point F is a midpoint of Line segment AB Point E is a midpoint of Line segment. Common point of triangle medians Theorem.

That is if ABC and D E F are the midpoints of the sides opposite A B C respectively then the segments AF BD CE all intersect in a common point G. The medians of a triangle are concurrent. The medians meet in an interesting point but its not equidistant from the vertices because the medians always meet inside the triangle.

One of the fascinating things about them is that no matter what shape the triangle all three always intersect at a single point. Any triangle has 3 medians Another answer depending on what you are looking for is that a triangle has concurrent medians which means all. Sum of medians of a triangle.

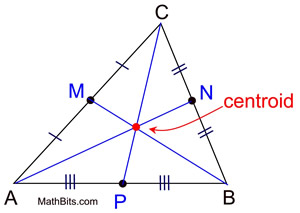
The three medians of a triangle intersect at a point called the centroid. This means that if you were to cut out the triangle the centroid is its center of gravity so you could balance it there. This point is called the centroid of the triangle.

Therefore the three medians intersect at a point. We know that medians trisect each other and that trisect point is called centroid. A Triangle ABC is an isosceles triangle with vertex at A.

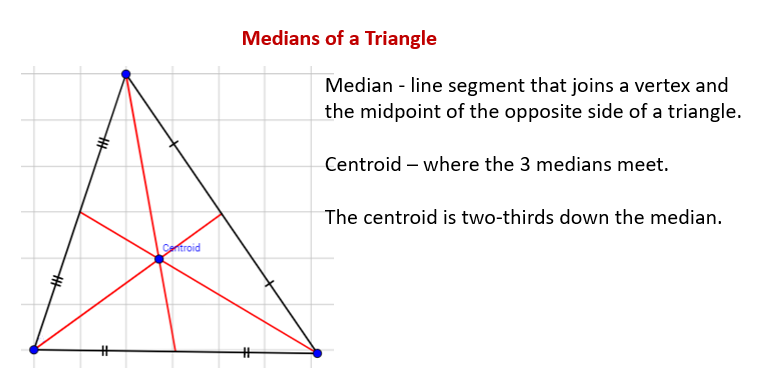
A point in which the three altitudes of the triangle intersect. It is possible for the orthocenter to occur on the triangle on the interior of the triangle or. In geometry a median of a triangle is a line segment joining a vertex to the midpoint of the opposite side thus bisecting that side.

Statements Justifications Point F is a. The triangle is divided into 6 smaller triangles of the same area by the centroid. What is the intersection of three medians in a triangle.

P B A C D F E THEOREM 49 The following theorem tells you that the three medians of a triangle intersect at one point. In an equilateral triangle the length of the medians is equal. In geometry a median of a triangle is a line segment joining a vertex to the midpoint of the opposite side thus bisecting that side.

The medians of a triangle are the segments drawn from the vertices to the midpoints of the opposite sides. The three corners of the triangle trace the three medians of the triangle. The medians of a triangle intersect each other in the ratio 21.

Each median of a triangle divides the triangle into two smaller triangles that have equal areas. The point where the three medians of a triangle intersect is called a centroid from the Latin word centrum-- center and the Greek suffix -oid-- like or similar to. The area of the triangle is divided into half by a median.

The idea of this proof is not correct. The medians of a triangle are concurrent in the internal part of a triangle. Symbols If P is the centroid of TABC then AP 5 2 3AD BP 5 2 3BF and CP 5 2 3CE.

The point of concurrency of three medians forms the centroid of the triangle. The centroid is the balancing point of a triangle. The medians are concurrent.

When written in the correct order the two-column proof below describes the statements and justifications for proving the three medians of a triangle all intersect in one point. A median of a triangle is a line segment from a vertex of the triangle to the midpoint of the side opposite that vertex. Determine the type of triangle.

Median Geometry Wikipedia